Équation de Mayo-Lewis

L'équation de Mayo-Lewis concerne l'obtention de copolymères diblocs par polyaddition. Elle sert à relier la composition instantanée du copolymère à la composition du mélange de monomères.

Catégories :

Polymère

L'équation de Mayo-Lewis concerne l'obtention de copolymères diblocs par polyaddition. Elle sert à relier la composition instantanée du copolymère (pourcentage d'unités A et B) à la composition du mélange de monomères (pourcentage de monomères A et B). Elle donne aussi une idée de la structure du copolymère : statistique, à bloc, alterné…

L'équation est la suivante :

$\frac {\mathrm{d}[A]} {\mathrm{d}[B]} = \frac {[A]}{[B]} \frac {r_A[A] + [B]} {r_B[B] + [A]}$

Les concentrations en monomères sont données entre crochets, $r A$ et $r B$ sont les rapports de réactivité.

Contexte et démonstration

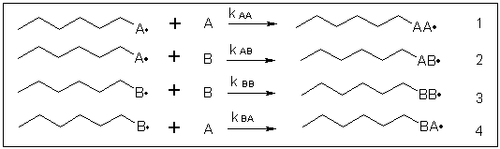
On synthétise un copolymère à partir des monomères A et B, en chaîne. À chaque addition d'un nouveau motif, on a quatre cas envisageables :

Possibilités lors d'une copolymérisation en chaîne

On cherche à savoir quelle sera la proportion des unités monomères issues de A et B dans le copolymère constitué. On peut écrire la vitesse de disparition des deux monomères :

$- \frac { \mathrm{d}[A] } { \mathrm{d}t } = k_{AA} [Aˆ\bullet][A] + k_{BA} [Bˆ\bullet][A]$
$- \frac { \mathrm{d}[B] } { \mathrm{d}t } = k_{BB} [Bˆ\bullet][B] + k_{AB} [Aˆ\bullet][B]$

Dans l'hypothèse de l'ÆQS, $k_{AB} [Aˆ\bullet][B] = k_{BA} [Bˆ\bullet][A]$ La concentration en centres actifs reste constante.
En faisant le rapport des deux vitesses de disparition en tenant en compte de cette cette égalité, on obtient : $\frac {\mathrm{d}[A]} {\mathrm{d}[B]} = \frac {[A]}{[B]} \frac {\frac {k_{AA}}{{k_{AB}}}[A] + [B]} {\frac {k_{BB}}{{k_{BA}}}[B] + [A]}$

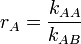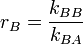On peut introduire les rapports de réactivité : $r_A=\frac {k_{AA}} {k_{AB}}$ et $r_B=\frac {k_{BB}} {k_{BA}}$ .
On aboutit à : $\frac {\mathrm{d}[A]} {\mathrm{d}[B]} = \frac {[A]}{[B]} \frac {r_A[A] + [B]} {r_B[B] + [A]}$
C'est l'équation de Mayo-Lewis^[1].

Calcul de composition

On définit les fractions molaires :

des unités monomères dans le copolymère constitué : $F_A = 1 - F_B = \frac {\mathrm{d}[A]} {\mathrm{d}[A] + \mathrm{d}[B]}$
des monomères dans le mélange de monomère : $f_A = 1 - f_B = \frac {[A]} {[A] + [B]}$

alors l'équation de Mayo-Lewis devient :

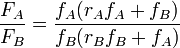
$\frac {F_A} {F_B} = \frac {f_A(r_Af_A + f_B)} {f_B(r_Bf_B + f_A)}$

À partir de cette relation, si on connait les rapports de réactivité, on peut calculer la composition d'un mélange de monomères à maintenir constante pour aboutir a un copolymère de composition donnée.

Répartition des motifs

Selon les valeurs des rapports de réactivité $r A$ et $r B$ , on peut avoir une idée de la structure du copolymère. Ainsi, si $<img class=$ k_AA > k_AB. dans ce cas, l'unité monomère A réagira préférentiellement sur elle-même plutôt que sur une unité B. Un certain nombre de cas limites existent.

$r A$ et $r B$ << 1: les unités réagissent préférentiellement sur l'autre type et on obtient un copolymère alterné : $(A - B - A - B - A - B - A - B - A - B - A - B) n$
$r A$ et $r B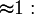$ $\mathbb{t} 1:$ : les unités réagissent sur elles-même ou sur l'autre sorte indifféremment. Le copolymère est statistique^[2] : $(A - B - B - A - B - B - B - A - A - B - A - A) n$
$r A > 1$ et $r B < 1$ : les unités de A réagissent entre elles et celles de b sur A aussi. Le copolymère enchaîne en particulier des unités A avec quelques accidents de B, jusqu'à ce que énormément d'unités A soient consommées : $(A - A - B - A - A - A - A - B - A - A - A - A - B)$ .
$r A > 1$ et $r B > 1$ : dans ce cas hypothétique la copolymérisation ne se ferait pas ou mal.

Calcul des rapports de réactivité

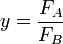Si on pose : $x = \frac {[A]}{[B]}$ et $y = \frac {F_A}{F_B}$ , l'équation de Mayo-Lewis devient :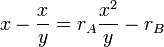 $x -\frac{x}{y} = r_A\frac{xˆ2}{y}-r_B$
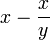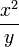On peut préparer des copolymères de compositions différentes et tracer $x -\frac{x}{y}$ selon $\frac{xˆ2}{y}$ . La courbe obtenue est une droite dont la pente et l'ordonnée à l'origine permettent de remonter aux rapports de réactivité. D'autres méthodes existent.

Références

Voir aussi

Copolymère

Recherche sur Google Images :

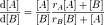
"en monomères sont données"
L'image ci-contre est extraite du site fr.wikipedia.org

Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur.

Voir l'image en taille réelle (196 × 47 - 2 ko - png)

Refaire la recherche sur Google Images

Recherche sur Amazone (livres) :

Principaux mots-clés de cette page : copolymères - monomères - unités - rapports - composition - réactivité - équation - mayo - lewis - mélange - pourcentage - idée - structure - statistique - concentrations - données - partir - chaîne - motif - copolymérisation -

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/%C3%89quation_de_Mayo-Lewis.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/12/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.