Rhéologie des solides
La rhéologie est une partie de la physique qui étudie la plasticité, l'élasticité, la viscosité et la fluidité caractéristiques des corps déformables.
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Les tests les plus fréquemment utilisés pour caractériser les propriétés rhéologiques des matériaux semi- solides sont : Etude de l'écoulement de matériaux... (source : malverninstruments)
- Rhéologie des solides exercices. Comportement mécanique de materiaux en pierre. Chaboche, lemaitre mécanique des matériaux solides... (source : priceminister)
La rhéologie est une partie de la physique qui étudie la plasticité, l'élasticité, la viscosité et la fluidité caractéristiques des corps déformables. Du grec reo (couler) et logos (étude).
Cet article concerne la rhéologie des solides, c'est-à-dire leur déformation, leur écoulement.
Propriétés mécaniques des solides
Lire l'article déformation élastique en guise d'introduction.
Contrainte et déformation
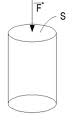
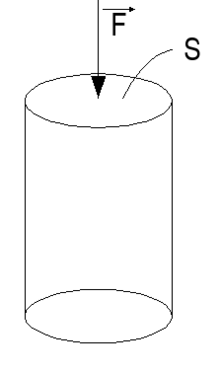
En physique, l'effort exercé sur une pièce est représenté par la force F, exprimée en Newton (N). La variation dimensionnelle est une longueur, exprimée en mètres.
Cependant, ceci dépend de la forme de la pièce. Si on s'intéresse aux propriétés du matériau, il faut s'abstraire des dimensions de la pièce. On caractérise par conséquent l'effort par la contrainte et la variation dimensionnelle par la déformation
- Contrainte
- Si S est la surface sur laquelle s'exerce la force F, on définit la contrainte σ
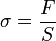
- La surface dépend de la déformation, mais pour les petites déformations, ceci est fréquemment négligé.
- Déformation
- Si L0 est la longueur d'origine de la pièce, alors la déformation ε est l'allongement relatif (sans unité)
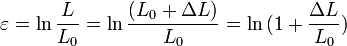
- Si la contrainte est faible alors la déformation est faible et donc
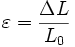
Propriétés du matériau
Lors de son utilisation, une pièce peut se déformer de manière complexe. Pour permettre l'étude, on considère des déformations modèles simples.
Ces déformations simples permettent de définir des caractéristiques chiffrées du matériau.
- Compression/traction uniaxiale
- module d'Young, noté Ec et exprimé en Pa ou plus fréquemment en GPa
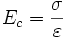
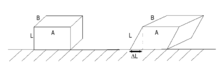
- Lors d'un étirement ou d'un raccourcissement, on constate un élargissement ou une contraction de la pièce, caractérisée par le cœfficient de Poisson ν (sans unité)
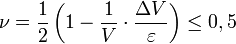
- Si ν = 0, 5 alors ΔV est faible comparé à ε ; exemples de valeur de cœfficient de Poisson :
- ν = 0, 5 : liquide
- ν = 0, 5 : caoutchouc
- ν = 0, 2 − 0, 35 : verre, polymère solide
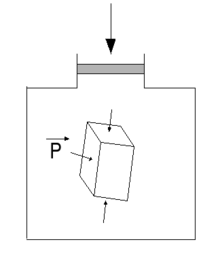
- Cisaillement
- module de cisaillement, noté G :
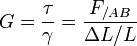
- complaisance de cisaillement, notée J :
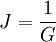
- Flexion
- combinaison de traction, compression, cisaillement.
- Compression isostatique (ou hydrostatique)
- module de compressibilité (bulk modulus) noté K :
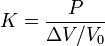
Relation entre les propriétés mécaniques
On a par conséquent quatre cœfficients E, G, B et ν, et deux relations. On peut alors écrire :
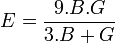
Types d'essais mécaniques
- Essais dynamiques : σ, ε fluctuent selon le temps
Viscoélasticité
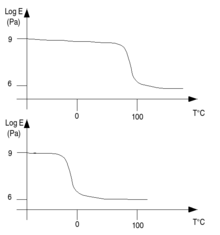
La viscoélasticité d'un corps dépend de sa température et du temps de repos. On note généralement :
On étudiera tandis qu'une de ses deux variables à la fois.
- Si on sollicite le solide, on le fera à température constante
- Si on fait fluctuer la température, on l'étudiera après un temps expérimental fixe.
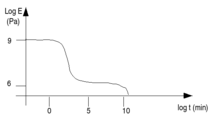
Ici on étudiera la relaxation qui est un phénomène réversible et détectable, se traduisant par une différence de mobilité moléculaire. Il ne faut pas la confondre avec la transition qui est un changement d'état physique (fusion, cristallisation, transition vitreuse... )
Principe de Boltzmann
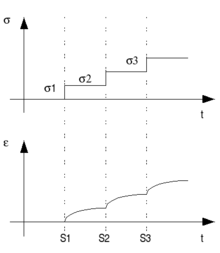
Selon Boltzmann, l'état de contrainte ou de déformation d'un corps viscoélastique dépend de l'ensemble des sollicitations appliquées au matériau.
Chaque nouvelle sollicitation contribue de manière indépendante à l'état final.
Les modèles rhéologiques de base
Corps parfaitement élastiques
- La réversibilité entre contrainte et déformation est idéale (il n'y a pas d'effet mémoire du matériau).
- Les relations entre contrainte et déformation sont instantanées.
- Les relations entre contrainte et déformation sont linéaires.
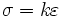
Le matériau peut être modélisé en mécanique par un ressort. Il n'y a aucune dissipation d'énergie.
Corps parfaitement visqueux
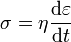
où η est la constante de Newton.
On a alors 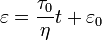 ici ε0 représente la déformation d'origine, par conséquent nulle.
ici ε0 représente la déformation d'origine, par conséquent nulle.
On obtient alors 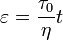 .
.
L'énergie est complètement dissipée sous forme calorifique. Le modèle équivalent en mécanique est celui d'un amortisseur.
Combinaison des modèles
Pour représenter le comportement viscoélastique des différents solides, on peut combiner ces deux modèles équivalents.
Maxwell
Le modèle de Maxwell rend compte du comportement viscoélastique et élastique d'un matériau mais pas de son comportement viscoplastique.
- à
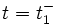 ,
, 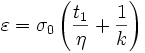
- à
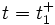 ,
, 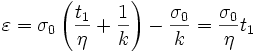
Voigt
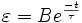
Zener
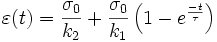 avec
avec 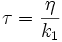
Burger
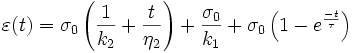 avec
avec 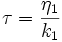
Dans ce modèle on a les trois composantes :
- élastiques avec
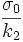
- viscoélastique avec
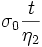
- viscoplastotique avec
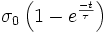
Comportement dynamique
Étude pratique de la rhéologie des solides
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/12/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

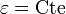 : Relaxation
: Relaxation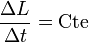 :
: 

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité