Loi de Hooke
La loi de Hooke est une loi de comportement élastique linéaire des solides soumis à une déformation de faible amplitude.
Recherche sur Google Images :
Source image : fr.academic.ru Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La loi de Hooke est une loi de comportement élastique linéaire des ... abrégé de la trace du tenseur des déformations (somme des termes... (source : jeuxvideo)
- La loi de Hooke est une loi de comportement des solides soumis à une déformation... du tenseur des déformations (somme des termes diagonaux du tenseur).... (source : techno-science)
- Un matériau obéissant à la loi de Hooke est dit élastique linéaire. On notera que cette définition n'est strictement valide que dans le cas de déformations... (source : books.google)
La loi de Hooke est une loi de comportement élastique linéaire des solides soumis à une déformation de faible amplitude.
Présentation
Cette loi de comportement a été énoncée par Robert Hooke, par la phrase en latin :
ce qui veut dire «telle extension, telle force», ou bien en termes modernes «l'allongement est proportionnel à la force». Hooke désirait obtenir une théorie des ressorts, en soumettant ces derniers à des forces croissantes successives. De sa loi deux aspects sont importants :
- La linéarité,
- L'élasticité.
Ces deux aspects ne sont pas semblables, la linéarité exprime «l'allongement est proportionnel à la force», l'élasticité exprime que cet effet est réversible et permet par conséquent de revenir a l'état d'origine tel un ressort soumis à de faible forces. L'élasticité a une limite, qui est indépendante de la notion de linéarité, Hooke n'a reconnu que la phase élastique et linéaire, par conséquent proportionnelle et réversible.
C'est en quelque sorte une ressemblance avec l'allongement 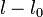 d'un ressort de constante de raideur
d'un ressort de constante de raideur 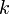 soumis à une force
soumis à une force 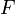 :
:
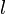 : longueur du ressort étiré ou comprimé ;
: longueur du ressort étiré ou comprimé ;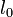 : longueur du ressort à vide.
: longueur du ressort à vide.
Pour un ressort on a
Pour s'abstraire de la forme de la pièce, et surtout de ses dimensions, on divise la force par l'aire de la section de la pièce, grandeur qu'on nomme contrainte σ (exprimée en Pa), et on divise l'allongement par la longueur d'origine, grandeur qu'on nomme déformation ou allongement relatif ε (sans dimension).
On note l'allongement relatif 
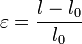 .
.
On note la contrainte 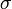 (homogène à une pression)
(homogène à une pression)
L'analogue de la constante de raideur du ressort est par conséquent le module de Young E.
La loi de Hooke s'exprime alors sous la forme :
où E est le module de Young, une caractéristique du matériau, loi valable pour l'étirement ou la compression d'une pièce, les autres dimensions étant libres de s'étendre.
La linéarité provient du fait qu'on est en faible déformation, on peut par conséquent faire une approximation linéaire de la loi réelle (développement limité au premier ordre). Il s'agit en fait d'approcher le potentiel interatomique par une parabole, voir l'article Déformation élastique > Pourquoi les lois sont-elles linéaires ?.
Dans le cas d'une pièce de forme complexe, la loi de déformation globale n'a aucune raison d'être linéaire, mais par contre, chaque élément illimitétésimal de matière se déforme lui de manière linéaire.
Loi de Hooke généralisée
Dans le cas d'un matériau isotrope, si on reprend en compte le cœfficient de Poisson ν, la loi de Hooke devient :
avec δij le symbole de Kronecker et εkk est une notation abrégé de la trace du tenseur des déformations (somme des termes diagonaux du tenseur).
On peut aussi l'écrire sous forme matricielle :
Les relations ci-dessus peuvent être inversées pour donner :
ou, sous forme matricielle (en appliquant la trace à la relation plus haut) :
La forme explicite particulièrement simple de ces relations (donnant les déformations suivant les contraintes)
montre bien la signification physique du module d'Young E et du cœfficient de Poisson ν.
Dans le cas d'un matériau anisotrope, on définit la contrainte et la déformation localement par un tenseur 3×3, le tenseur des contraintes [σij] et le tenseur des déformations [εij]. Le comportement élastique du matériau est alors modélisé par un tenseur d'ordre 4 ![\left[ C_{ijkl} \right]](illustrations/e8573664366230fac7b90f09450a9223.png) contenant 81 cœfficients élastiques. Le nombre de cœfficients indépendants est réduit à 21 en tenant compte de la symétrie des tenseurs de contraintes et de déformations, et de la stabilité énergétique du tenseur. On a :
contenant 81 cœfficients élastiques. Le nombre de cœfficients indépendants est réduit à 21 en tenant compte de la symétrie des tenseurs de contraintes et de déformations, et de la stabilité énergétique du tenseur. On a :
en appliquant la sommation sur les indices (Convention de sommation d'Einstein).
Du fait de ces propriétés de symétrie, le tenseur Cijkl peut être représenté sous la forme d'une matrice 6x6, où les directions représentent les directions de la déformation.

Pour simplifier l'écriture, on adopte fréquemment une notation de 1 à 6, nommée notation de Voigt, avec les axes de compression/traction notés de 1 à 3 et les axes de cisaillement notés de 4 à 6.
Utilisation culturelles
Ut tensio sic vis est la devise de l'École Polytechnique de Montréal.
Voir aussi
- Cœfficients d'élasticité
- Plasticité et endommagement des polymères
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/12/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

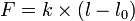
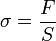
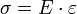
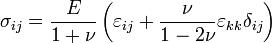
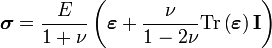
![\varepsilon _{ij}=\frac{1}{E}\left[ \left( 1+\nu \right) \sigma _{ij}-\nu\sigma_{kk}\delta _{ij}\right]](illustrations/c8e47675b32fecaf8e86647634973fea.png)
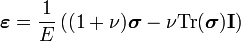
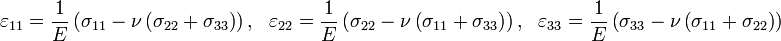
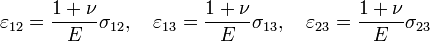
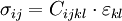

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité