Déformation élastique
La déformation élastique est une déformation réversible : le milieu retourne à son état d'origine quand on supprime les sollicitations.
Recherche sur Google Images :

Source image : fr.academic.ru Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La gamme d'élastique finit lorsque le matériel atteint le son force de rendement. En ce moment la déformation en ... (source : worldlingo)
- ... Si la déformation est élastique, on a toujours proportionnalité entre la force appliquée par unité de section et l'allongement relatif... (source : michel.hubin.pagesperso-orange)
- On peut définir simplement la contrainte comme étant une force appliquée à une certaine... À un point donné durant la déformation élastique, la relation... (source : ggl.ulaval)
La déformation élastique est une déformation réversible : le milieu retourne à son état d'origine quand on supprime les sollicitations.
La déformation élastique est un domaine important de la mécanique des milieux continus (MMC) et de la thermodynamique (compression des gaz).
L'élasticité linéaire concerne les petites déformations proportionnelles à la sollicitation. Dans cette gamme, l'allongement est proportionnel à la force dans le cas d'un étirement, et l'angle est proportionnel au couple dans le cas d'une torsion.
Aux plus grandes déformations, l'élasticité devient non linéaire pour certains matériaux. Pour d'autres, la fracture ou le fluage interviennent. Voir plus bas.
La notion d'élasticité n'est pas spécifique à la mécanique des milieux continus et en physique, en général, on parle d'interaction élastique quand il y a la conservation d'une grandeur. A titre d'exemple, dans un choc élastique, les objets s'échangent leur énergie cinétique, mais il n'y a pas de perte par frottement ou par déformation résiduelle (de fait, la déformation est élastique). Dans le cas de l'interaction d'un atome avec un rayonnement électromagnétique, on parle de diffusion élastique quand le rayonnement conserve la même longueur d'onde (diffusion Rayleigh).
Cas des gaz
Un gaz est constitué de molécules qui volent et s'entrechoquent. Elles se cognent aussi aux parois du récipient contenant le gaz, ce qui crée la pression. L'énergie cinétique moyenne d'une molécule est proportionnelle à la température absolue (en Kelvin) :
k étant la constante de Boltzmann.
La pression du gaz sur les parois dépend par conséquent du nombre de chocs par seconde et de la force de chaque choc, cette force dépendant de l'énergie cinétique. Si on diminue le volume de l'enveloppe en désormais la température constante (compression isotherme), on augmente la fréquence des chocs par conséquent la pression. À l'inverse, si on agrandit l'enveloppe, on diminue la fréquence des chocs, et par conséquent on diminue la pression. Ceci se retrouve dans les lois de comportement des gaz, par exemple dans la loi des gaz parfaits, la pression est inversement proportionnelle au volume :
(la constante de proportionnalité vaut nRT où n est la quantité de gaz et R est la constante des gaz parfaits). Si on prend un cylindre de section S constante et de longueur l variable par l'action d'un piston, on a
soit pour de petites variations (développement limité de la fonction  autour de l0) :
autour de l0) :
qui est une loi linéaire (ou plutôt affine) en l.
On a bien un comportement élastique pour les gaz isothermes soumis à de faibles variations de volume.
Voir les articles Théorie cinétique des gaz et Pression cinétique.
Déformation élastique des solides
Exemple des ressorts
Le cas le plus simple de déformation élastique est celui des ressorts.
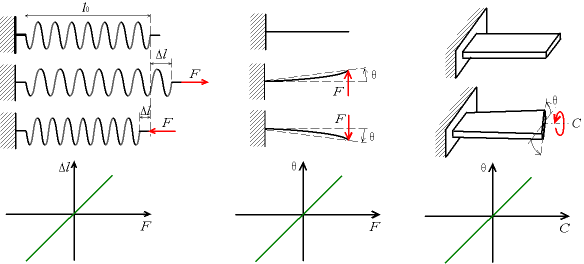
Trois exemples de ressorts : ressort à spires non-jointives sollicité selon son axe (fig. de gauche), ressort à lame sollicité en flexion (au centre), ressort à lame sollicité en torsion (à droite)
Sur les dessins, nous n'avons pas représenté la réaction du support auquel est accroché le ressort. Mais il faut bien voir que la déformation résulte de l'application de deux actions mécaniques opposées (forces et/ou couples) ; s'il n'y a qu'une seule force, en application du principe essentiel de la dynamique, la force accélère le ressort sans provoquer de déformation, on se ramène à la mécanique du point.
Quand les lois de déformation sont linéaires, le cœfficient de proportionnalité est nommé raideur du ressort et est noté k :
- F = k1 · Δl pour une traction-compression ;
- F = k2 · θ pour une flexion ;
- C = k3 · θ pour une torsion.
On remarque que les cœfficients k1, k2 et k3 ne sont pas homogènes (ils n'ont pas la même dimension). L'angle θ doit être exprimé en radians.
Dans le cas d'un ressort à spires non-jointives, l'énergie de déformation élastique W est le travail de la force :
C'est par conséquent la surface du triangle délimité par la droite dans le graphique (Δl, F), soit
- W = 1/2 k1 Δl 2 = 1/2 · F · Δl
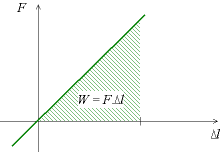
Illustration graphique de l'énergie de déformation élastique dans le cas d'un ressort à spires non-jointives
Note : sur la première figure, nous avons utilisé un graphique montrant la déformation selon la force, par exemple (F, Δl). Sur la seconde figure, nous avons inversé les axes et représenté la force selon la déformation (Δl, F). Si la première représentation nous semble plus intuitive (on se représente la force comme la cause de la déformation), les deux sont équivalentes. C'est de fait la seconde, (Δl, F), qui est la plus utilisée, les essais de traction se faisant à déformation imposée croissante (voir l'explication dans l'article essais mécaniques).
Limite d'élasticité
La déformation élastique intervient pour les faibles sollicitations. Si on augmente les sollicitations, on change le mode de déformation :
- rupture (endommagement) pour les matériaux dits «fragiles» :
- déformation plastique (irréversible et non linéaire) puis rupture pour les matériaux dits «ductiles» ;
- peut-être fluage pour les matériaux ductiles si la vitesse de déformation est lente et la température élevée.
La contrainte délimitant le domaine élastique des autres domaines est nommée limite d'élasticité (yield strength en anglais).
Contrainte et déformation
On utilise deux modèles de déformation élastique : la traction-compression et le cisaillement. La flexion peut se modéliser selon les cas comme une traction-compression ou comme un cisaillement, la torsion se modélise comme un cisaillement (voir plus bas).
Traction-compression uniaxiale
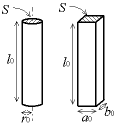
Prenons le cas de la traction ou de la compression d'une pièce cylindrique ou parallélépipédique selon son axe. La traction-compression correspond à des forces s'exerçant perpendiculairement aux sections de ces pièces ; elle est dite uniaxiale car les côtés de la pièce ne sont pas contraints, l'ensemble des forces sont sur un même axe.
Allongement dans l'axe
En prenant des pièces de différentes dimensions, on remarque que pour une force donnée :
- l'allongement Δl est proportionnel à la longueur d'origine l0 du cylindre ;
- ceci se conçoit bien : si on met deux ressorts semblables bout-à-bout, le premier ressort transmet totalement la force au second ressort, les deux s'allongent par conséquent de la même quantité ; par conséquent si avec un ressort on a un allongement Δl1, avec deux ressorts l'allongement total est 2Δl1 ;
- l'allongement Δl est inversement proportionnel à la section du cylindre ;
- on conçoit aussi facilement que si on met deux ressorts semblables en parallèle, chaque ressort exercera la moitié de la force de traction, l'allongement final sera par conséquent Δ1/2 ; si on double la section de la pièce, c'est comme si on mettait deux pièces côte-à-côte.
Si on veut caractériser le matériau en faisant abstraction de la forme de la pièce et de ses dimensions, on définit donc :
- l'allongement relatif ou déformation (strain en anglais), noté ε
-
- ε est sans dimension, on l'exprime quelquefois en % (100×Δl/l0)
- la contrainte (stress en anglais), notée σ
-
- σ est homogène à une pression ; du fait des valeurs énormes mises en jeu, on l'exprime le plus souvent en mégapascal (MPa).
La loi élastique s'écrit alors :
- σ = E ε
c'est la loi de Hooke ; E est le module de Young (Young's modulus en anglais), qui est une caractéristique du matériau. E est aussi homogène à une pression, du fait des valeurs particulièrement élevées qu'il prend, il est le plus souvent exprimé en gigapascal (GPa).
On voit facilement que la densité d'énergie de déformation w, c'est-à-dire l'énergie élastique divisée par le volume de la pièce, vaut :
- w = 1/2 · σ · ε = 1/2 · E ε²
Élargissement
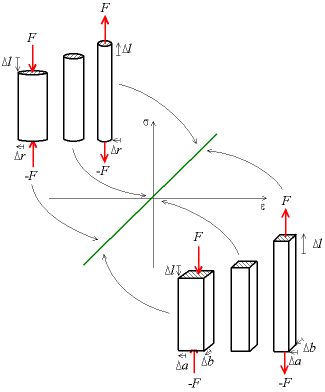
Quand on exerce une traction ou une compression, on constate que la largeur de la pièce fluctue aussi, à l'inverse de l'allongement. La variation relative de dimension est proportionnelle à l'allongement relatif ε, le cœfficient de proportionnalité se nomme le cœfficient de Poisson ou rapport de Poisson (Poisson's ratio en anglais) en hommage au mathématicien français Siméon Denis Poisson. Il est noté ν et est sans unité :
- pour un cylindre :
- pour un parallélépipède rectangle :
Considérons le volume de la pièce. Pour une pièce cylindrique, on a :
- V = l × π r 2
Pour des petites variations, on a donc :
- ΔV/V0 = Δl/l0 + 2·Δr/r0
(développement limité au premier ordre), soit :
- ΔV/V0 = (1 - 2ν) · ε
De même pour une pièce parallélépipédique, on a :
- V = l × a × b
- ΔV/V0 = Δl/l0 + Δa/a0 + Δb/b0
donc de même :
- ΔV/V0 = (1 - 2ν) · ε
On voit par conséquent que :
- si ν > 0, 5 le volume diminue en traction et augmente en compression (cas exceptionnel) ;
- si ν < 0,5 le volume augmente en traction et diminue en compression (comportement le plus général).
Pour un acier, ν vaut à peu près 0, 3, on est par conséquent dans le second cas.
Si désormais on maintient la largeur constante — par exemple on effectue une compression mais la pièce est dans une gaine ultra-rigide et ne peut pas s'étendre —, alors, la déformation n'est plus uniaxiale, la gaine exerce une pression (une contrainte) sur les côtés de la pièce. Il faut alors utiliser un autre cœfficient élastique, noté C11, différent de E :
- σ = C11 · ε
Cisaillement
Si on considère un parallélépipède rectangle, le cisaillement est une variation de l'angle, qui n'est plus droit. Cela correspond à des forces s'exerçant parallèlement à la face.
On définit de même la contrainte comme étant la force divisée par la surface sur laquelle elle s'exerce ; cette contrainte est nommée cission (toujours exprimée en MPa) et est notée τ.
La déformation est l'écart à l'angle droit γ, nommé cisaillement, exprimé en radian.
On a toujours une loi linéaire :
- τ = G · γ
où G est le module de cisaillement ou module de Coulomb, le plus souvent exprimé en GPa. Dans le cas d'un milieu isotrope, le module de cisaillement est lié au module d'Young et au cœfficient de Poisson par la relation suivante :
Note : dans l'article Tenseur des déformations, l'angle γ défini vaut la moitié de l'angle γ défini ici.
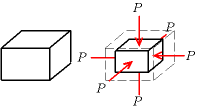
Compression isostatique
Une compression isostatique est l'exercice d'une pression isotrope, c'est-à-dire qui a la même valeur dans l'ensemble des directions. Si on sert à désigner par V le volume de l'objet, la variation de volume relative est proportionnelle à la variation de la pression P :
où K est le module d'élasticité à la compression isostatique[1] (bulk modulus en anglais). On remarque que K est l'inverse du cœfficient de compressibilité isotherme χT défini en thermodynamique par :
K est aussi homogène à une pression et est le plus souvent exprimé en gigapascal (GPa). On a :
| matériau | K |
|---|---|
| acier | 160 GPa |
| eau | 2, 2 GPa |
| air | 0, 000 1 GPa[2] |
Dans le cas d'un milieu isotrope, le module d'élasticité isostatique K, le module de Young E et le module de cisaillement G sont liés par la relation suivante :
Cas des grandes déformations
La définition qu'on a prise de ε dépend du trajet suivi. Considérons une déformation finale de ε1 + ε2. Si on fait la déformation en une étape, la longueur finale est
- l = l0 (1 + ε1 + ε2)
Si par contre on déforme en premier lieu de ε1, on a une première longueur
- l = l0 (1 + ε1)
qui devient la longueur d'origine pour l'étape suivante, par conséquent quand on rajoute une déformation ε2, on obtient
- l = l0 (1 + ε1) (1 + ε2)
En développant cette dernière formule, on voit que les deux sont équivalentes si
- ε1 · ε2 ≪ ε1 et ε1 · ε2 ≪ ε2
soit, de manière synthétique, si
- ε² ≪ ε, soit ε ≪ 1 ;
c'est l'hypothèse des petites déformations.
Pour les grandes déformations, on peut utiliser une autre définition de ε :
on voit que si l et l0 sont proches, le développement limité de cette formule redonne la définition de ε des petites déformations
Pourquoi les lois sont-elles linéaires ?
Généralement, toute loi peut localement (c'est-à-dire pour de petites variations) se remplacer par un développement limité du premier ordre, ou «approximation linéaire», à condition que la tangente de la loi ne soit pas horizontale autour du point reconnu. Les lois élastiques sont par conséquent des approximations linéaires du comportement réel, plus complexe.
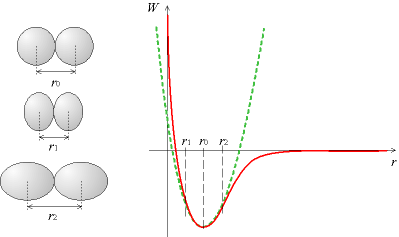
Plus exactement, l'explication de la linéarité se trouve dans la forme du potentiel interatomique W (r), où r est la distance entre deux atomes.
À une température de 0 K, la distance entre deux atomes est r0. Si on s'éloigne légèrement de cette valeur, l'énergie W augmente ; on peut localement approcher la loi de W par une parabole (il s'agit en fait d'un développement limité au second ordre), on peut par conséquent écrire :
- W (r) = W0 + k · (r - r0) 2.
La force étant la dérivée de l'énergie potentielle, on voit que les atomes sont soumis à une force de rappel (qui tend à faire revenir à r0) qui vaut :
- F = 2k · (r - r0)
qui est bien une loi linéaire.
Déformations complexes
Nous avons vu jusqu'ici des exemples de déformation simples : traction uniaxiale, cisaillement, compression isostatique, sur un parallélépipède rectangle. Les applications réelles correspondent à des pièces et des sollicitations plus complexes, nécessitant de décrire la déformation et les contraintes par des matrices, des tenseurs, voir les articles :
Notes
- La notion de module de compressibilité est d'ambiguë dans la mesure où il s'agit de l'inverse de la dite compressibilité.
- l'équation des gaz parfaits nous donne χT = 1/P, soit K = P = 105 Pa = 10-4 GPa à une atmosphère.
Voir aussi
Liens externes
- Théorie de l'élasticité des corps solides, É. Mathieu (1835-1890), Traité de physique mathématique (sur Gallica)
- tenseurs contrainte/déformation - loi de comportement élastique isotrope, orthotrope manuel de référence du logiciel de calcul de structure ICAB Force
- Tutoriel sur la déformation élastique d'une structure de poutres en nid d'abeille, Univ. Cambridge.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/12/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

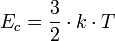
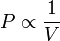
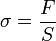
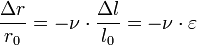
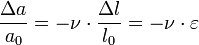
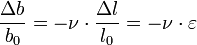
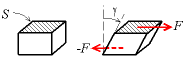
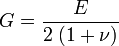
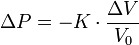
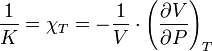
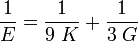
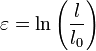

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité